Mathematical Structures

Mathematical Structures

Exploring Natural Growth Patterns in Bio-Data Flow

Jun 2022

computationmathematical-formgeometry

rhinograsshoppermilipedeparakeetkaramba3dgalapagosanaconda

Details

DigitalFUTURES International Workshop: Individual work

Contributor

Arnott Ferels

Abstract

This study integrates bio-data with mathematical structural dynamics to investigate how nature’s imprints manifest on mathematical surfaces. Emphasizing adaptability and modularity, tools like Rhino, Grasshopper, and Milipede are employed to transform natural growth patterns into 3D architectures. As the study unfolds, it incorporates optimization mechanisms, notably the Galapagos plugin and K-means Clustering in machine learning. This fusion of traditional and contemporary techniques provides a comprehensive, data-informed perspective in the field of computational design.

Instructor

Mahdi Fard; Crispina Ken; Patrish Kumar

Cite

BibTeX

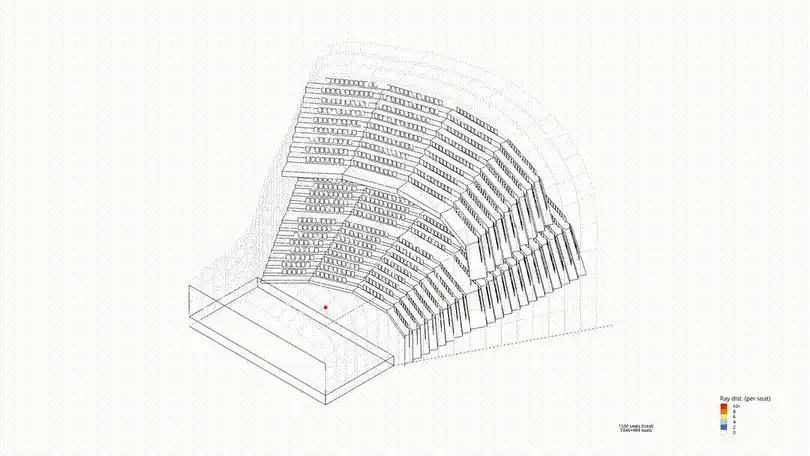
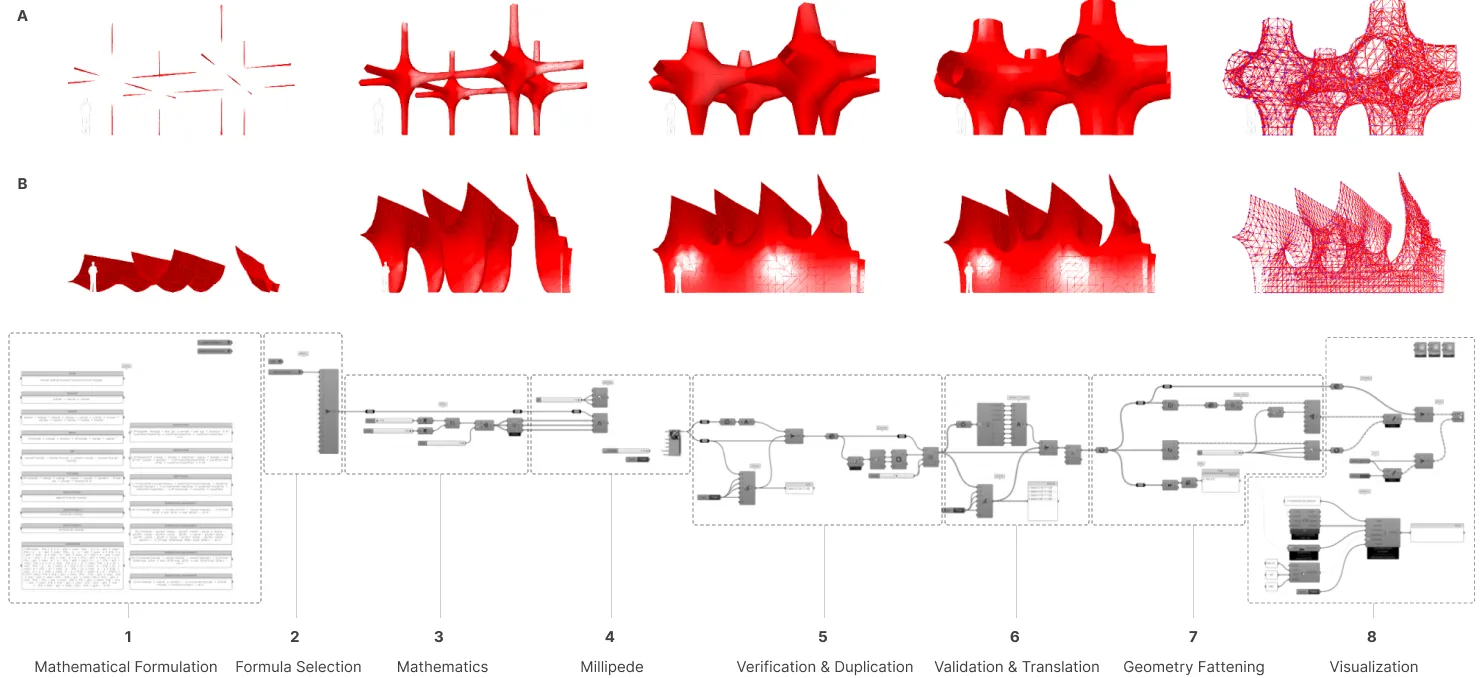
Exploring Architectural Mathematical Surface/Minimal Surfaces
Generating Structures: Venation/Growth Patterns
Designing & Optimizing: Iterative Structural Analysis
Clustering Results – K-means Approach

Exploring Architectural Mathematical Surface/Minimal Surfaces

This section combines bio-data and mathematical dynamics to understand how nature influences mathematical surfaces.

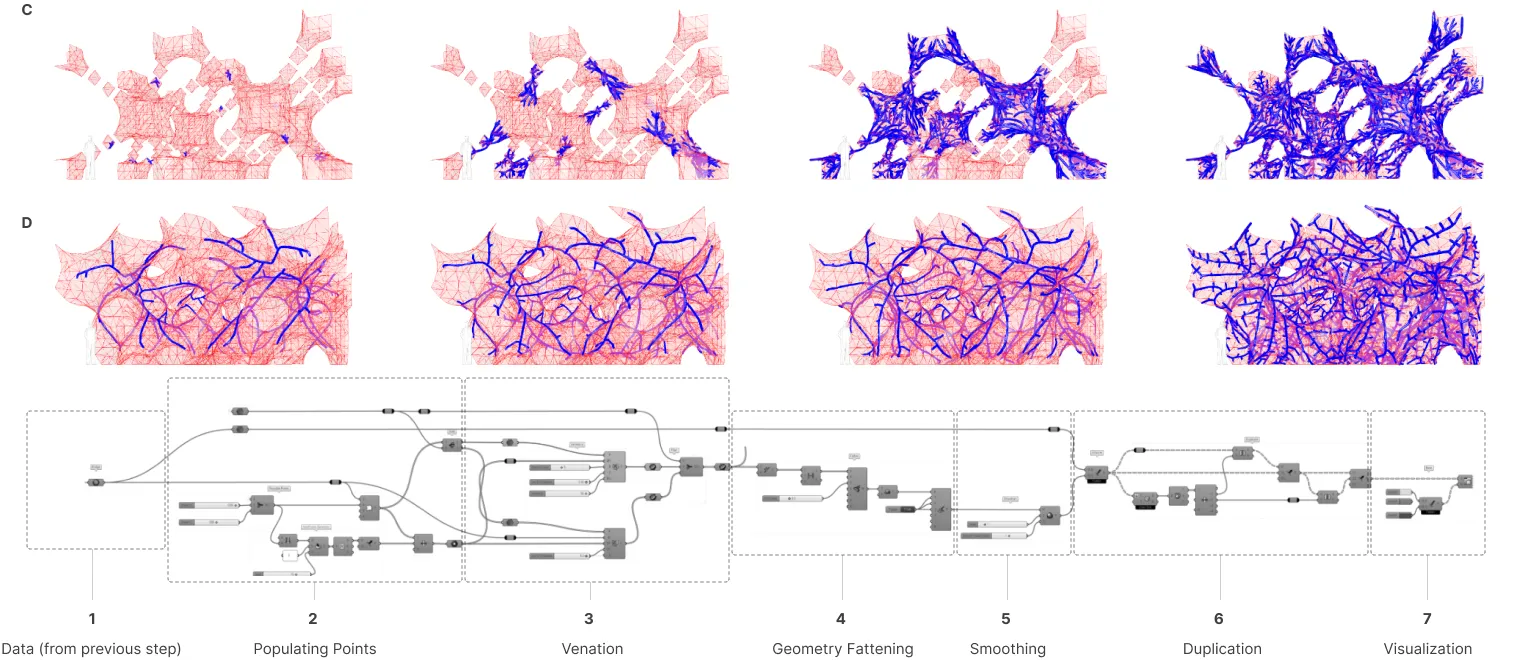
Generating Structures: Venation/Growth Patterns

This section utilizes tools like Rhino and Grasshopper with Parakeet to translate nature’s growth patterns into architectural forms, focusing on the intricacies of venation and organic development.

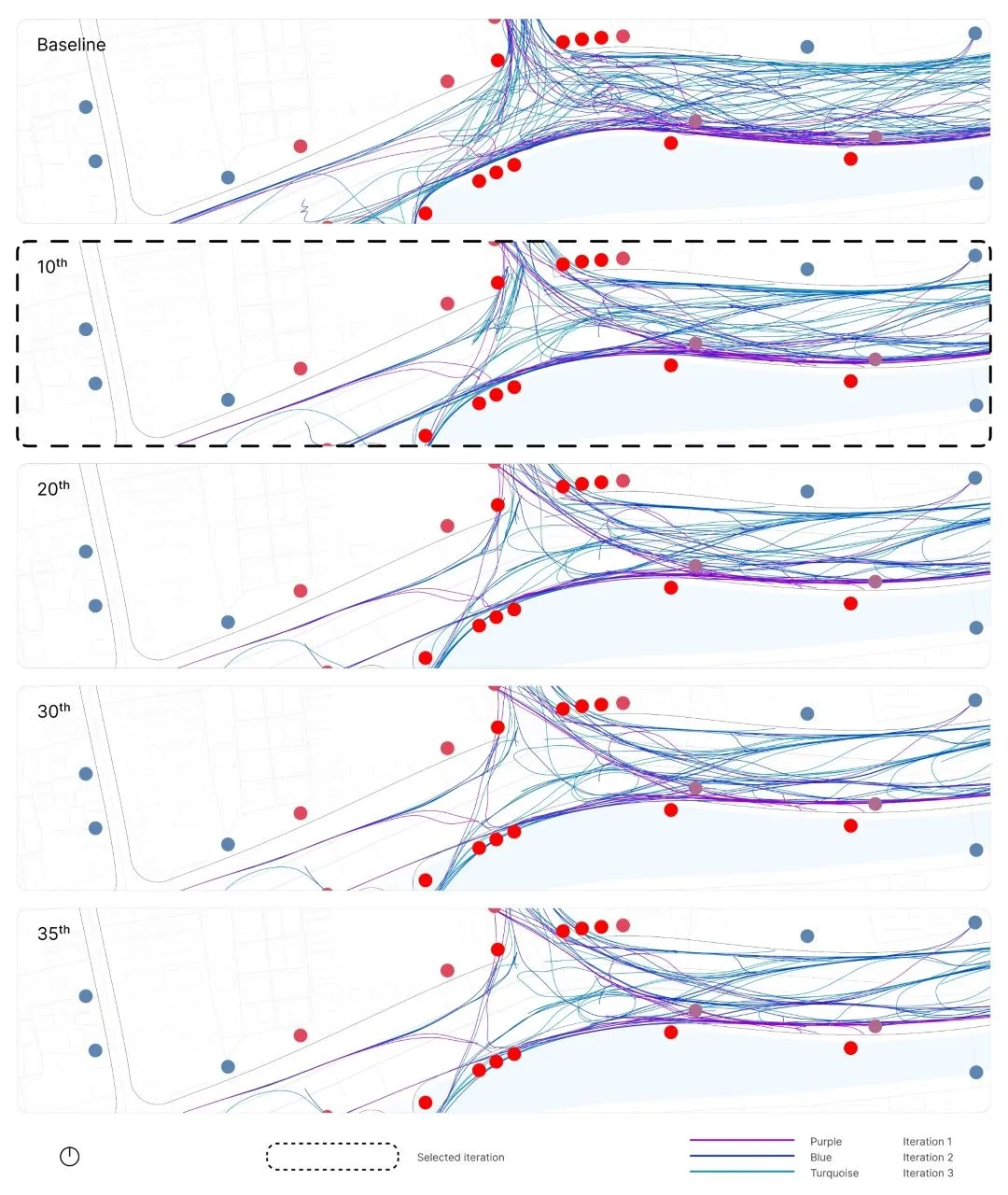
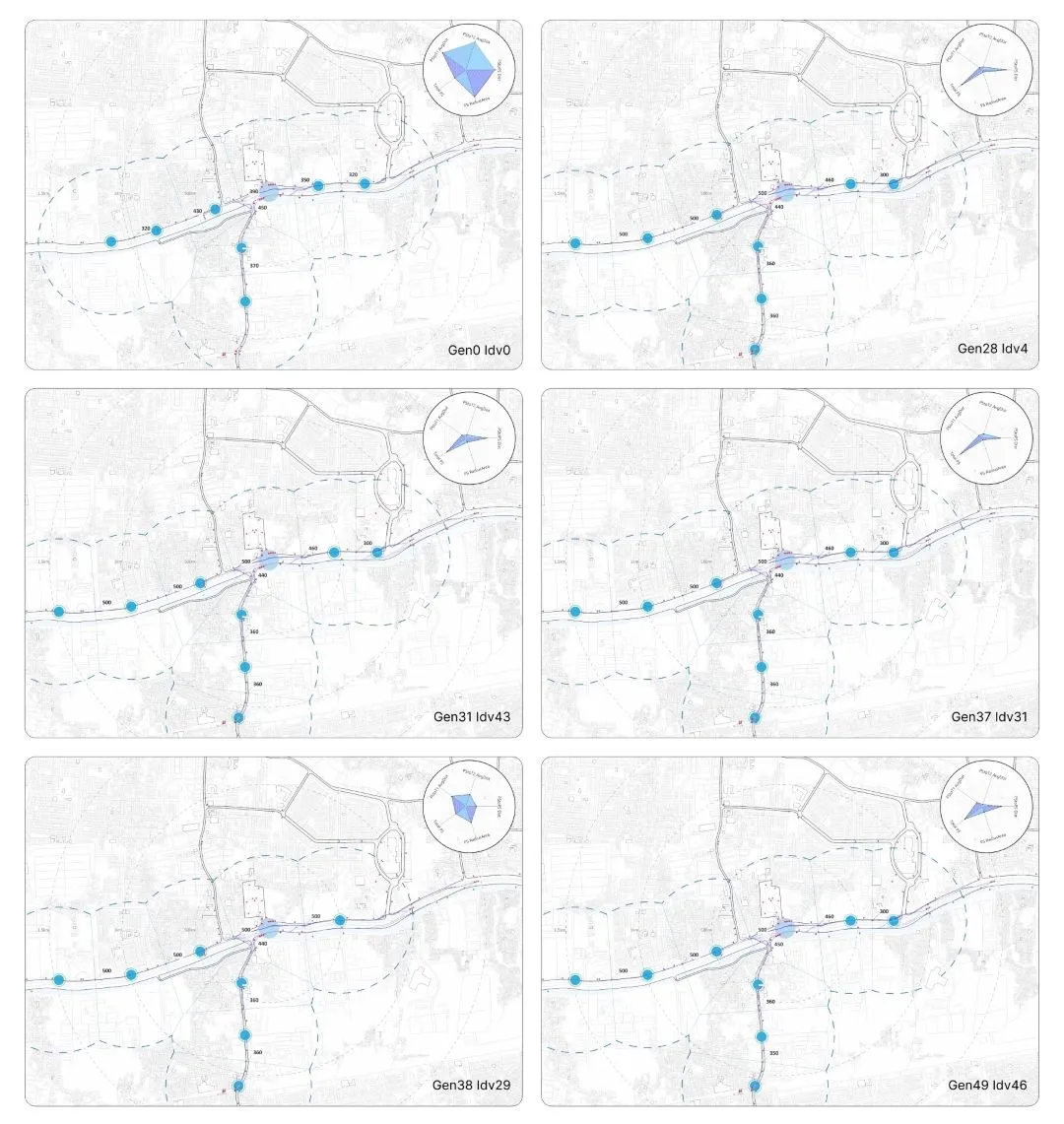
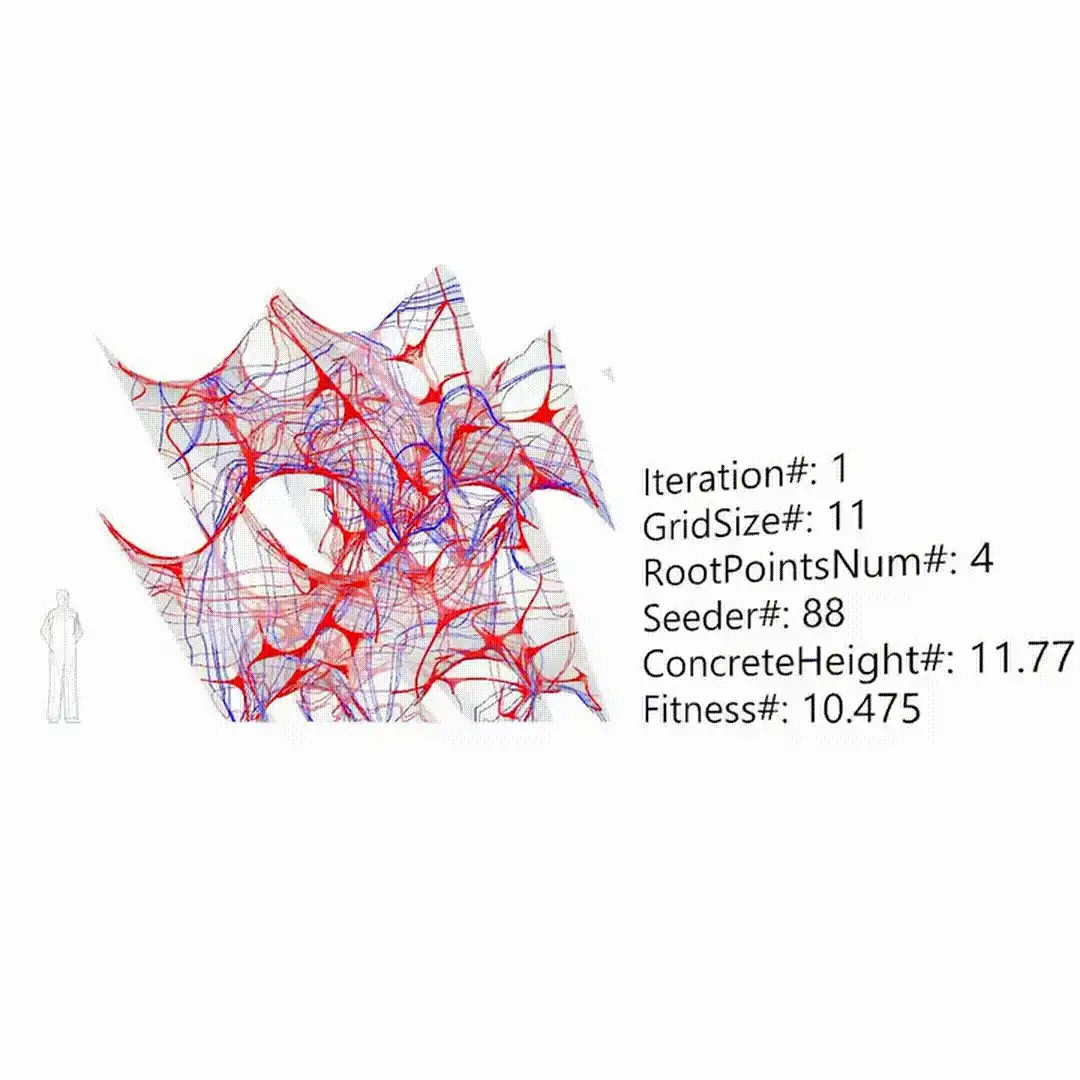
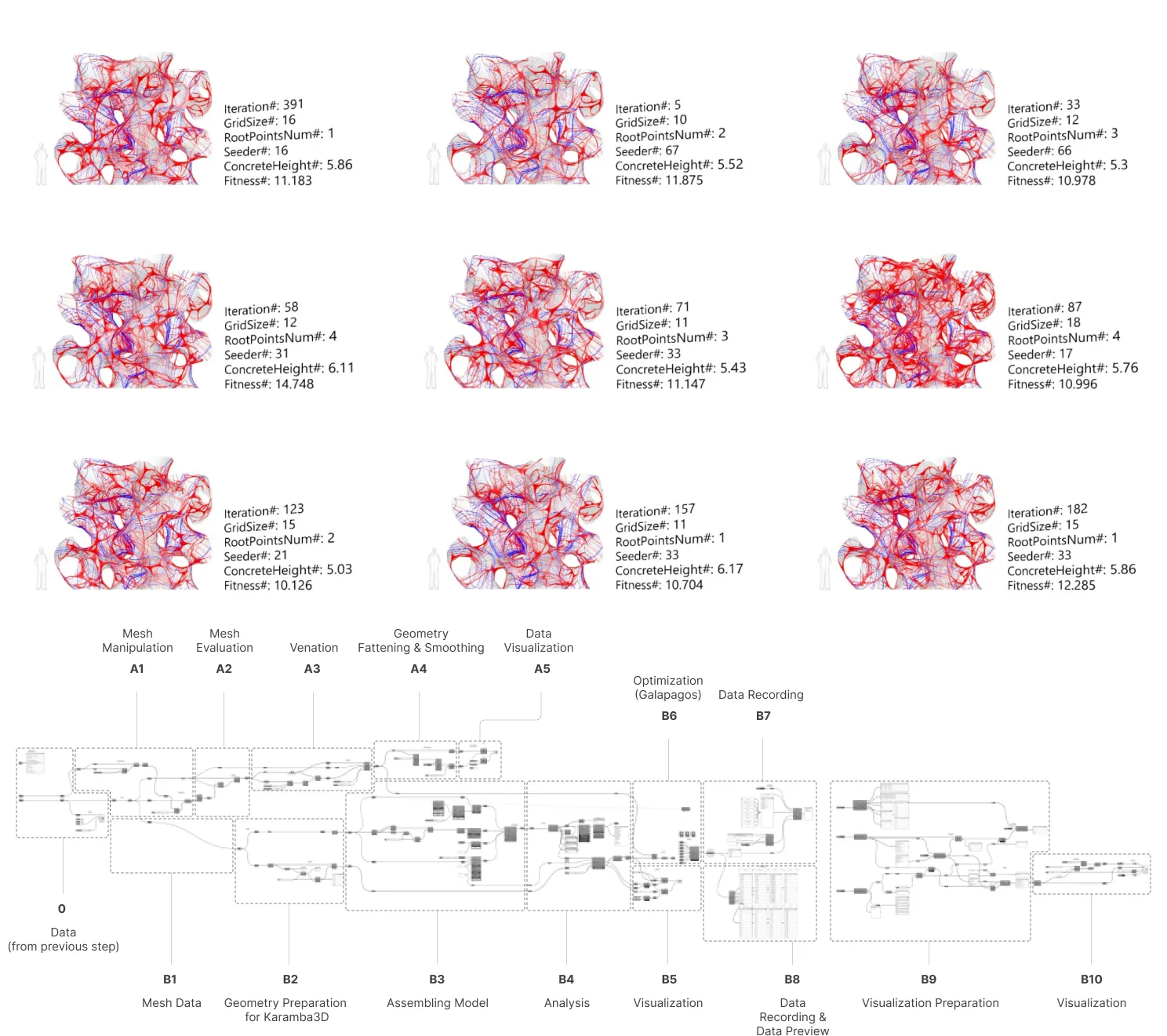
Designing & Optimizing: Iterative Structural Analysis

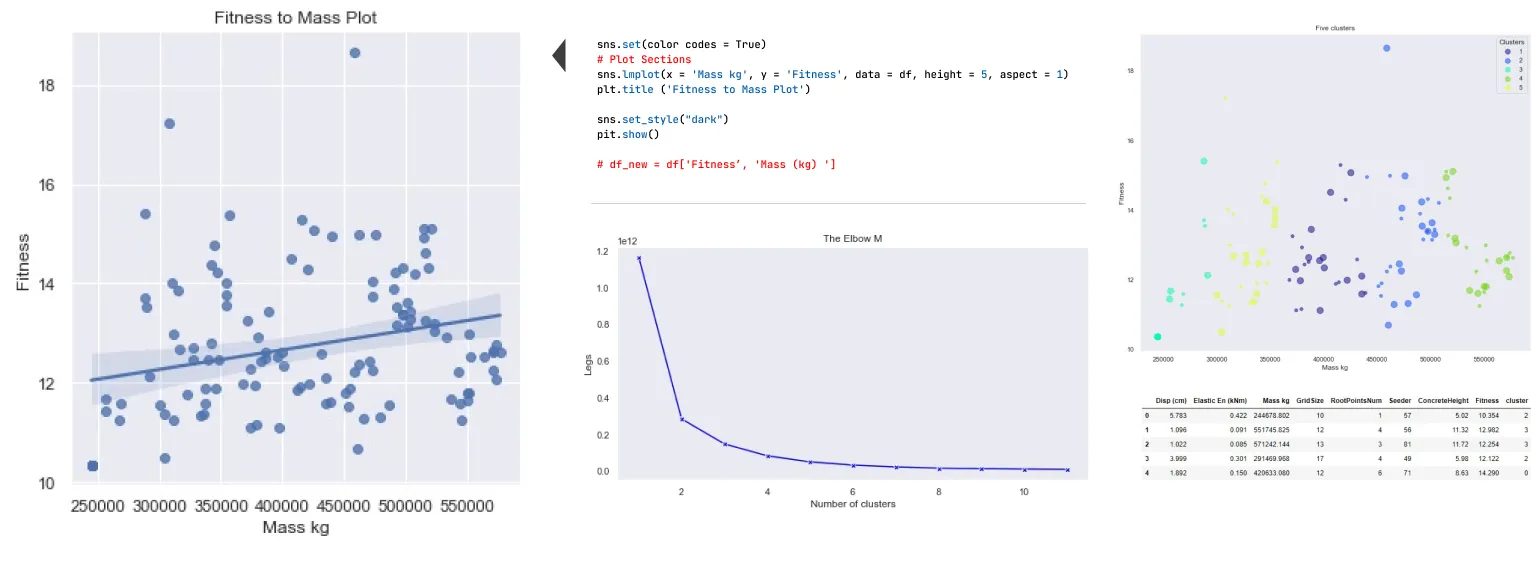
This section delves into the process of refining designs post-structural analysis. Utilizing tools like Karamba and Galapagos, iterative adjustments of key parameters such as grid size, root points, and concrete height contribute to a purposeful trajectory towards architectural excellence. Each iteration, guided by predefined objectives and a fitness metric, ensures resulting structures meet both aesthetic standards and functional requirements.

Clustering Results – K-means Approach

This section employs the K-means Clustering technique within the Anaconda Jupyter environment, a machine learning approach. This methodology enhances the precision of the analysis of design elements, classifying and improving design outputs.