Walkability model dengan metode Dynamic Multi-Layer pada desain Transit Hub di Jakarta Barat

Walkability model dengan metode Dynamic Multi-Layer pada desain Transit Hub di Jakarta Barat

Jan 2023

dynamic-multi-layer-methodagent-based-modelingshortest-path-algorithm-a-starlaplacian-smoothingevolutionary-multi-objective-optimizationdata-clusteringtransit-hubpublic-space

Details

Publisher

Architecture ITB

Course

Thesis

Advisor

Aswin Indraprastha

Jury

M. Donny Koerniawan; Heru W. Poerbo

Cite

BibTeX

Konten

Informasi
A. Lampiran
- A.1. Referensi teori non-arsitektural
Informasi
Referensi

Informasi

Akses teks lengkap di situs ini: Teks lengkap.

A. Lampiran

A.1. Referensi teori non-arsitektural

Bagian ini membahas teori non-arsitektural yang digunakan dalam tesis ini, termasuk clustering data (distilasi dan subset data), Laplacian smoothing (LS), Shortest Path Algorithm (SPA) dan Algoritma A-star (A*), serta algoritma NSGA-2 dan Pareto front (PF).

A.1.1. Distilasi dan subset data

A.1.1.1. Prinsip dan proses distilasi data

Distilasi data mengurangi data berulang menjadi satu single set. Ini digunakan untuk membangun profil baru, misalnya di perbankan untuk menentukan suku bunga baru atau di manufaktur untuk memilih material terbaik (Inmon et al., 2020).

A.1.1.2. Prinsip dan proses subset data

Setelah distilasi, data disaring lebih lanjut menjadi subset untuk menghindari bias dan mempermudah analisis. Ini membantu memilih data yang relevan dan menarik (Inmon et al., 2020).

A.1.2. LS

A.1.2.1. Definisi dan prinsip kerja LS

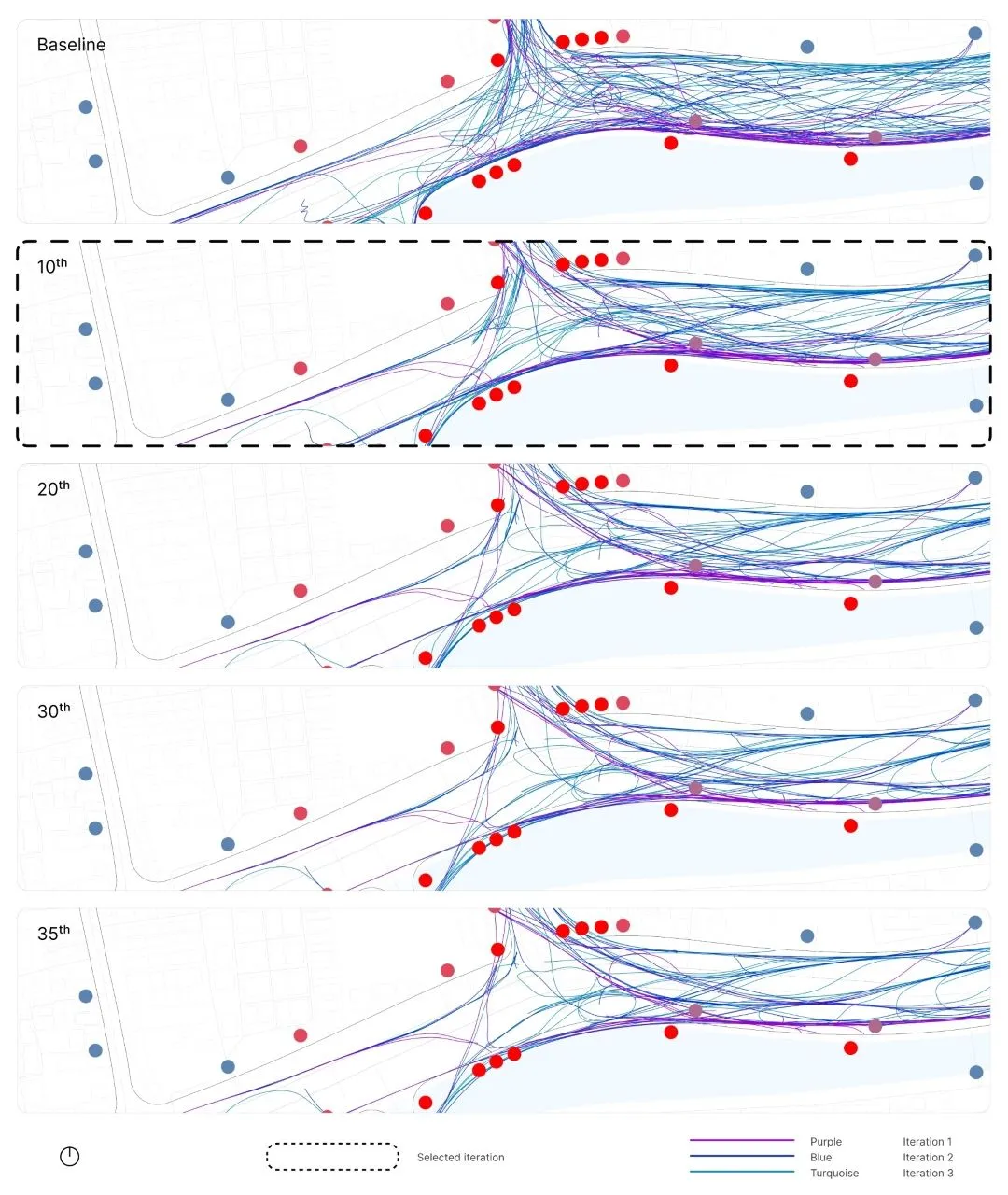
LS adalah algoritma berbasis geometri yang mengatur ulang dan memperhalus mesh dengan menyesuaikan posisi simpul (nodes). Ini meningkatkan kualitas mesh tanpa mengubah tipologi awalnya (Huang et al., 2020; Xiao et al., 2019).

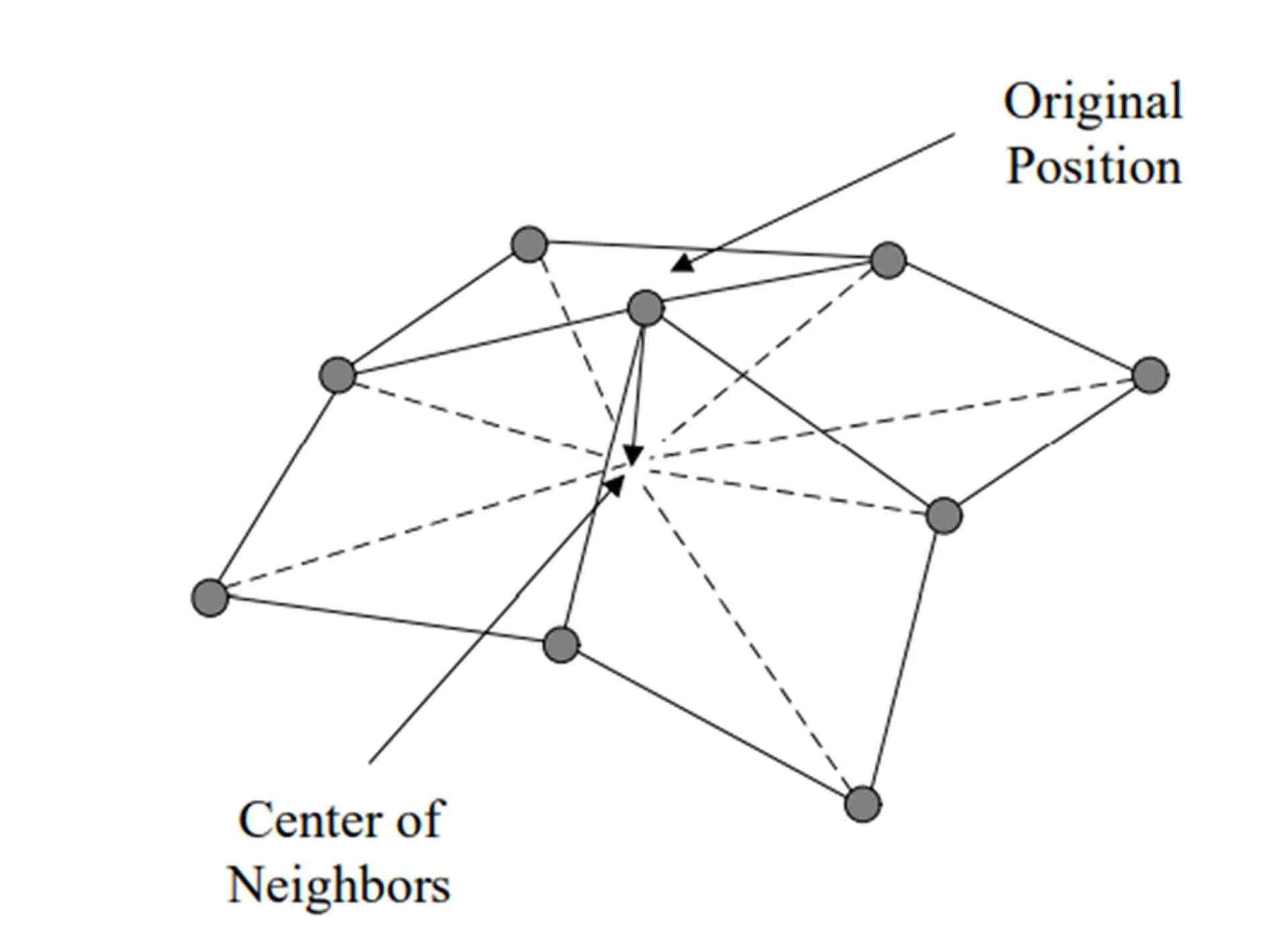
Ilustrasi sederhana penggunaan LS (Xiao et al., 2019). — Ilustrasi sederhana penggunaan LS (Xiao *et al.*, 2019).

A.1.2.2. Proses iterasi LS

Dalam penyesuaian ulang, titik A adalah koordinat awal, dan titik B adalah koordinat akhir yang dihitung secara iteratif berdasarkan titik sebelumnya (Xiao et al., 2019).

\overline{x_i^{(q+1)}} = \frac{1}{n} \sum_{j=1}^{N} x_j^q \tag{A.1}

Di mana $N$ adalah jumlah node tetangga, dan $\overline{x_i^{(q+1)}}$ adalah koordinat baru setelah penghalusan dan iterasi $(q+1)$ (Xiao et al., 2019).

\overline{x_i^{(q+1)}} = \frac{1}{n} \left( \sum_{j=1}^{N} x_j^q + \sum_{k=1}^{N_{q+1}} x_k^{(q+1)} \right), \quad \begin{cases} 0 \leq N_q \leq N \\ 0 \leq N_{(q+1)} \leq N \\ N_q \leq N_{(q+1)} \leq N \end{cases} \tag{A.2}

Di mana $N_q$ dan $N_{(q+1)}$ adalah nilai turunan dari $q$ dan $(q+1)$ . Jika $N_{(q+1)} = 0$ , maka Persamaan A.1 berlaku (Xiao et al., 2019).

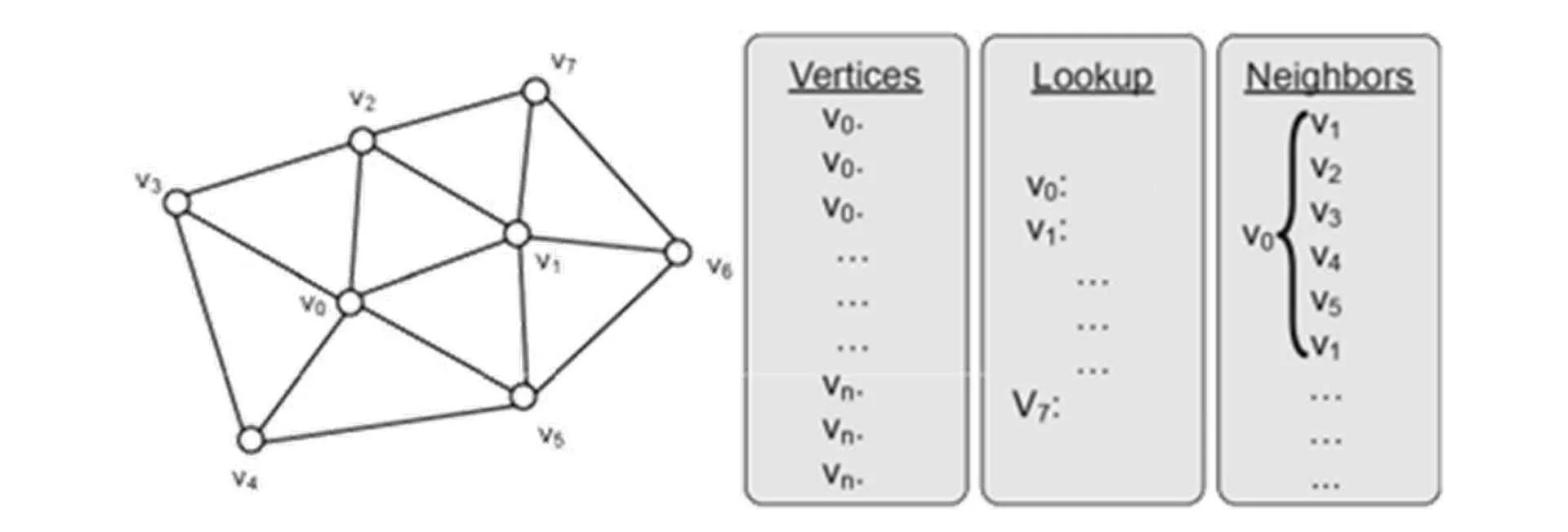
Menurut Mönc dkk. (2012), LS membutuhkan titik koordinat (vertices), titik pencarian (lookup), dan daftar tetangga terdekat (neighbors) (Preim et al., 2014). — Menurut Mönc dkk. (2012), LS membutuhkan titik koordinat (*vertices*), titik pencarian (*lookup*), dan daftar tetangga terdekat (*neighbors*) (Preim *et al.*, 2014).

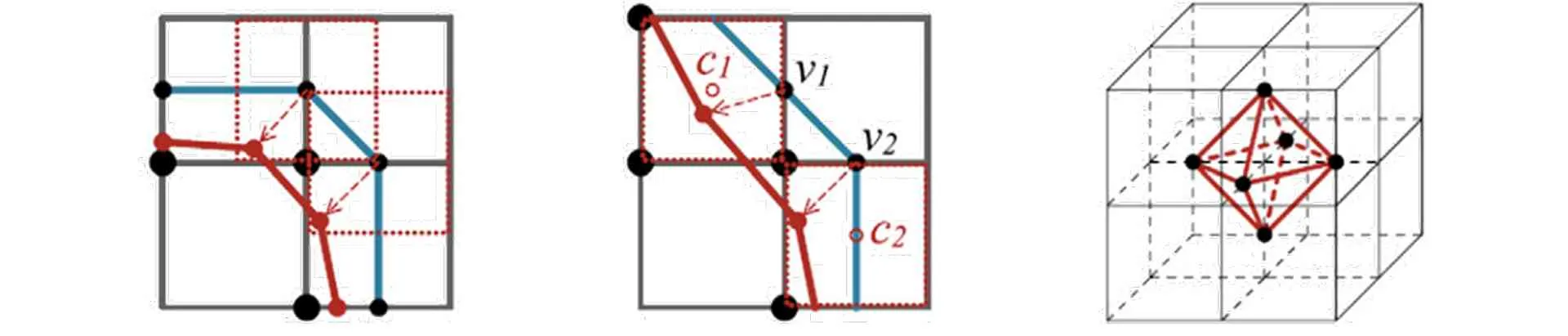
Contoh LS tingkat lanjut pada bentuk 3D berbasis koordinat awal (Ragnar Bade, University of Magdeburg) (Preim et al., 2014). — Contoh LS tingkat lanjut pada bentuk 3D berbasis koordinat awal (Ragnar Bade, University of Magdeburg) (Preim *et al.*, 2014).

A.1.2.3. Tujuan dan penerapan LS

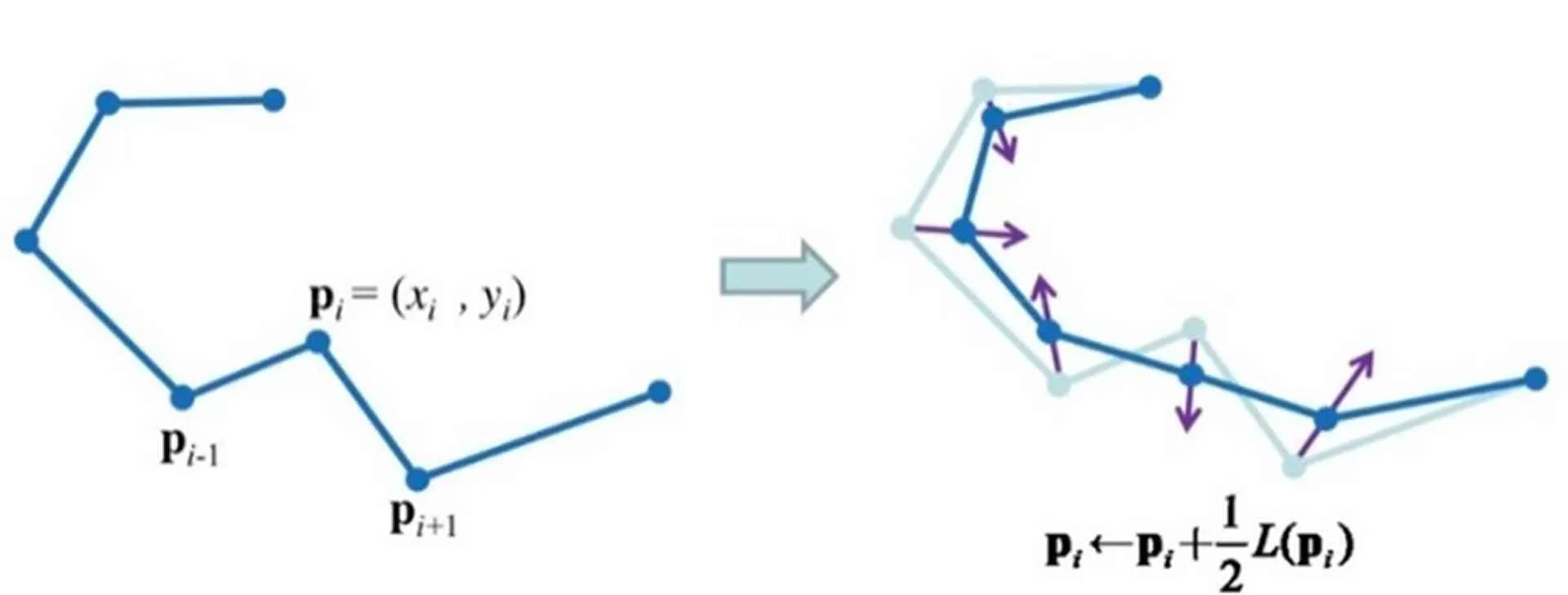
Ilustrasi proses iteratif LS: hubungan node dan tetangga (Li, 2018).

LS dapat diterapkan dalam pemodelan geometris menggunakan perangkat lunak seperti Rhino dan Grasshopper. Meskipun tidak memiliki pustaka aljabar linier, iterasi algoritma memungkinkan pengguna menghasilkan model dengan keseimbangan antara akurasi dan kecepatan solusi. LS juga fleksibel dan dapat diterapkan dalam berbagai tahap desain (Huang et al., 2020).

A.1.3. Shortest path algorithm (SPA) dan algoritma A*

A.1.3.1. Sejarah SPA dan A*

SPA lahir dari kebutuhan menyelesaikan pemodelan jejaring (network) untuk menemukan rute terpendek.

1955 – Dantzig merumuskan masalah rute terpendek.
1957 – Minty mengembangkannya menggunakan representasi web string dan knots.
1959 – Ford memperkenalkan metode panjang busur negatif.
1959 – Dijkstra menyederhanakannya dengan penyimpanan data minimal, yang hingga kini masih digunakan.
1968 – Hart dkk. mengembangkan Algoritma A* yang menggabungkan estimasi biaya “penyelesaian rute”.

Dalam 50 tahun terakhir, pendekatan A* terus disempurnakan dan digunakan dalam optimasi rute telepon, jaringan komunikasi, dan sistem transportasi (Zeng and Church, 2009).

A.1.3.2. Fungsi dan kelebihan A*

Proses SPA antara fungsi-fungsi definitif (Schneider et al., 2011). — Proses SPA antara fungsi-fungsi definitif (Schneider *et al.*, 2011).

A* digunakan untuk mencari rute terpendek dengan menyesuaikan jalur terhadap jaringan yang ada (Schneider et al., 2011).

Optimasi dapat dilakukan menggunakan algoritma evolusioner seperti Galapagos.
Keunggulan A* dibandingkan Dijkstra:
- Mencari solusi sub-optimal, bukan hanya optimal.
- Lebih cepat dan efisien dalam pencarian terarah ([^Alieksieiev/2019]; [^Mittal-etal/2021]).

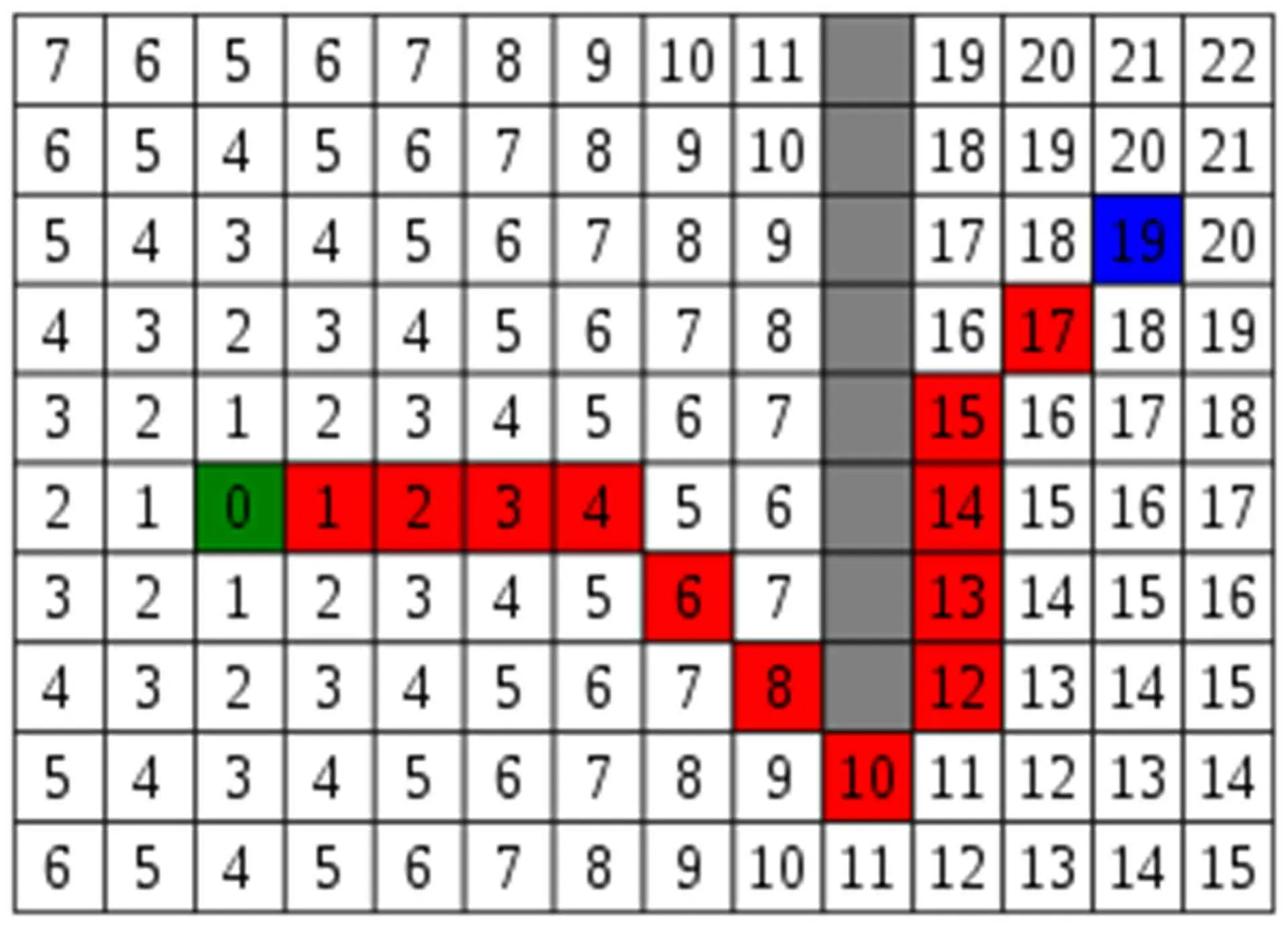
A.1.3.3. Proses kerja A*

A* mengoptimalkan pencarian dengan menggabungkan fungsi heuristik $h(n)$ dan biaya aktual $g(n)$ (Hart et al., 1968).

f(n) = g(n) + h(n) \tag{A.3}

$g(n)$ – Rute aktual terpendek dari titik awal $s$ ke node $n$ .
$h(n)$ – Estimasi jarak dari node $n$ ke tujuan $a$ .
$f(n)$ – Total biaya terpendek sementara; akan diperbarui sampai algoritma selesai.

A.1.4. NSGA-2, dan PF

NSGA-2 dikembangkan oleh Deb dkk. dan merupakan salah satu algoritma evolusi multi-objektif (MOO) yang paling banyak digunakan (Deb et al., 2000; Deb et al., 2002).

Perbaikan dari NSGA klasik:
- Mengurangi parameter berbagi (shared parameter).
- Menambahkan elitism dalam seleksi.
- Menggunakan non-dominated sorting yang lebih efisien.

Solusi Pareto front: min-min, min-max, max-min, max-max (Akbari et al., 2014). — Solusi Pareto front: *min-min*, *min-max*, *max-min*, *max-max* (Akbari *et al.*, 2014).

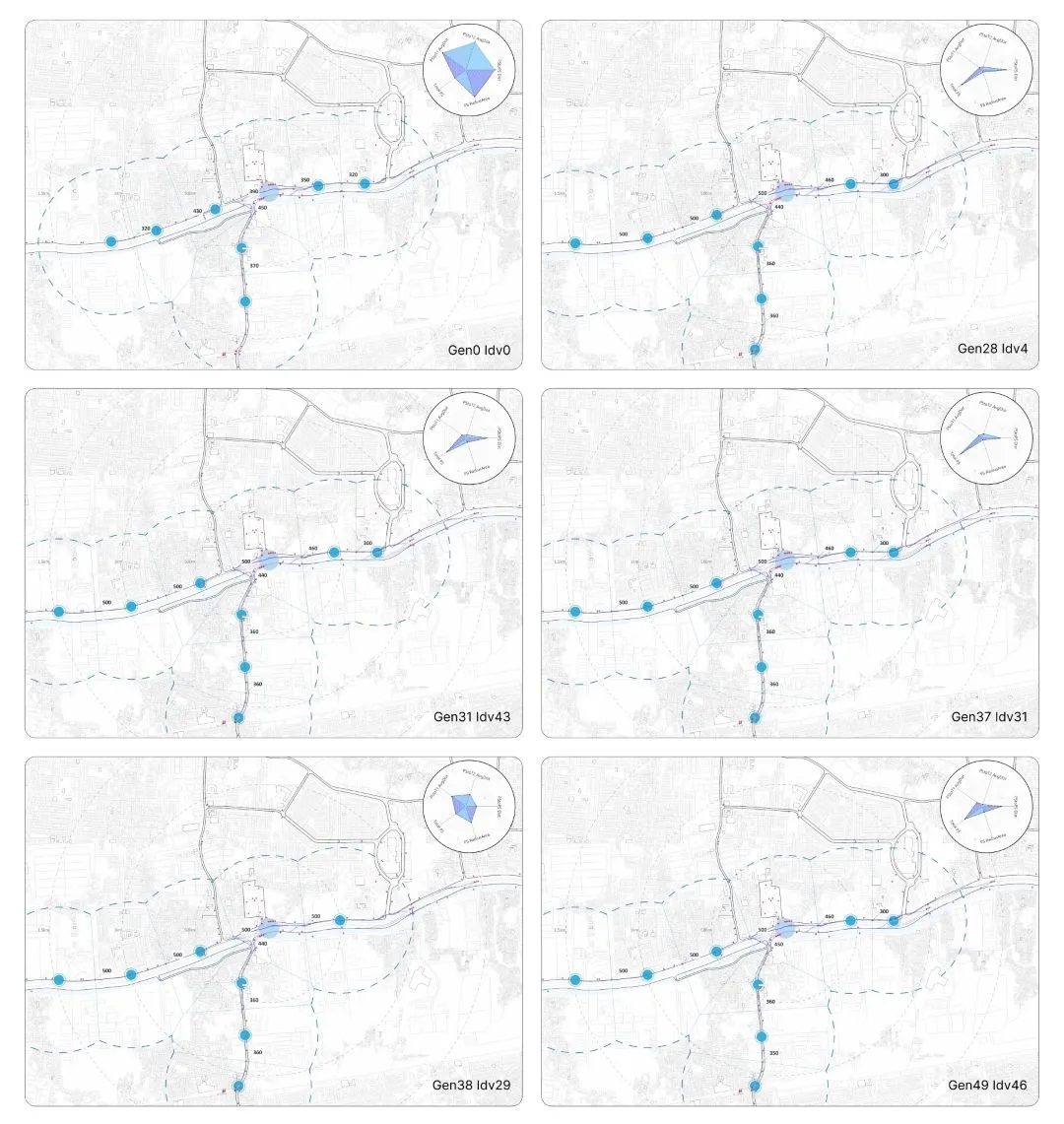
Salah satu aplikasi yang mendukung NSGA-2 adalah Wallacei X, yang bekerja dengan algoritma generatif dan menampilkan hasilnya secara visual melalui grafik analitik (Huang et al., 2022).

A.1.4.1. Wallacei

Wallacei dikembangkan oleh Mohammed Makki dalam studi doktoralnya di Architectural Association (AA) dengan promotor Dr. Michael Weinstock (Makki et al., 2019).

Berbasis komputasi evolusioner untuk pemecahan masalah desain.
Memiliki 3 fokus utama:
1. Formulasi desain (problem formulation).
2. Analisis hasil (output analysis).
3. Pemilihan solusi optimal (optimized solution selection).

A.1.4.2. Analisis data Wallacei

Wallacei menghasilkan berbagai jenis grafik analitik, antara lain:

SDG – Standard Deviation Graph (visualisasi tiap FO secara real-time).
SDT – Standard Deviation Trendline (garis tren deviasi standar untuk semua generasi).
MVT – Mean Value Trendline (garis tren nilai rata-rata).
PCP – Parallel Coordinate Plot (visualisasi PCP dari generasi pertama hingga terakhir).
DF – Diamond Fitness Chart (grafik DF untuk solusi terpilih).
FVG – Fitness Values Graph (grafik nilai kebugaran tiap solusi dalam populasi).

Diagram Wallacei Analytics oleh Chi Thanh Phat Nguyen dan Jason Choi, Studio Magister Arsitektur UTS (Makki et al., 2019). — Diagram Wallacei Analytics oleh Chi Thanh Phat Nguyen dan Jason Choi, Studio Magister Arsitektur UTS (Makki *et al.*, 2019).

A.1.4.3. Proses simulasi Wallacei

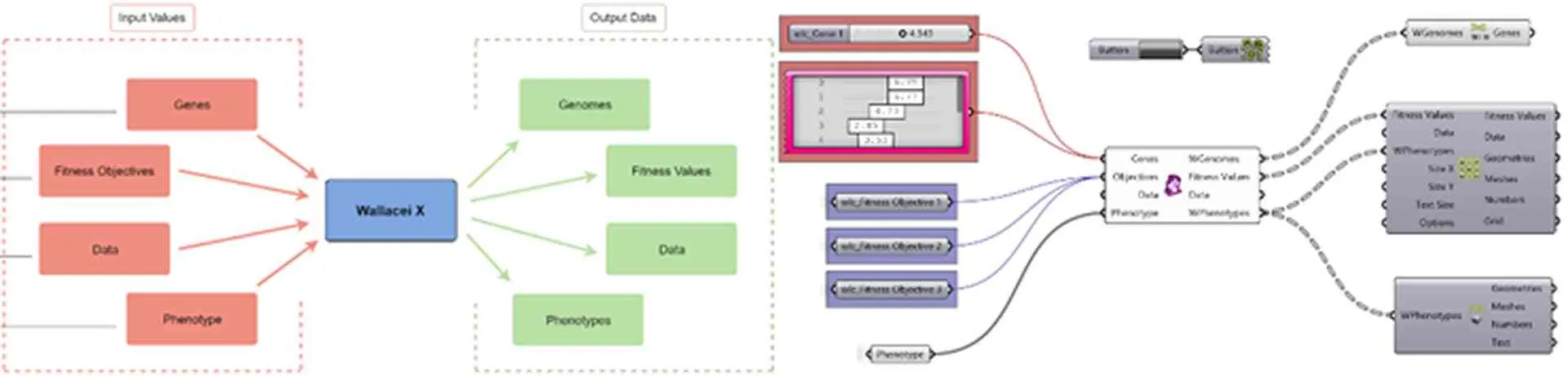
Alur kerja Wallacei X dalam Grasshopper 3D (Makki et al., 2019). — Alur kerja Wallacei X dalam Grasshopper 3D (Makki *et al.*, 2019).

Pada tahap input values, data yang diperlukan: Genes; Fitness Objectives/FO; Data; Phenotypes. Setelah diproses dalam Wallacei X, output values: Genomes; Fitness Values/FV; Data; Phenotypes.

Informasi

Akses teks lengkap di situs ini: Teks lengkap.

Referensi

Akbari, M., Asadi, P., Besharati Givi, M. K., dan Khodabandehlouie, G. (2014): 13 - Artificial neural network and optimization (Woodhead Publishing Series in Welding and Other Joining Technologies), 543–599 dalam M. K. B. Givi dan P. Asadi, ed., Advances in Friction-Stir Welding and Processing, Woodhead Publishing. https://doi.org/10.1533/9780857094551.543 ⌃
Deb, K., Agrawal, S., Pratap, A., dan Meyarivan, T. (2000): A Fast Elitist Non-dominated Sorting Genetic Algorithm for Multi-objective Optimization: NSGA-II, Parallel Problem Solving from Nature PPSN VI, Springer, Berlin, Heidelberg, 849–858. https://doi.org/10.1007/3-540-45356-3_83 ⌃
Deb, K., Pratap, A., Agarwal, S., dan Meyarivan, T. (2002): A fast and elitist multiobjective genetic algorithm: NSGA-II, IEEE Transactions on Evolutionary Computation, 6(2), 182–197. https://doi.org/10.1109/4235.996017 ⌃
Hart, P. E., Nilsson, N. J., dan Raphael, B. (1968): A Formal Basis for the Heuristic Determination of Minimum Cost Paths, IEEE Transactions on Systems Science and Cybernetics, 4(2), 100–107. https://doi.org/10.1109/TSSC.1968.300136 ⌃
Huang, C., Zhang, G., Yao, J., Wang, X., Calautit, J. K., Zhao, C., An, N., dan Peng, X. (2022): Accelerated environmental performance-driven urban design with generative adversarial network, Building and Environment, 224, 109575. https://doi.org/10.1016/j.buildenv.2022.109575 ⌃
Huang, Z., Ding, J., dan Xiang, S. (2020): Suspension Footbridge Form-Finding with Laplacian Smoothing Algorithm, International Journal of Steel Structures, 20(6), 1989–1995. https://doi.org/10.1007/s13296-020-00396-4 ⌃ ⌃²
Inmon, W. H., dan Linstedt, D. (2015): 7.1 - Repetitive Analytics – Some Basics, 231–248 dalam W. H. Inmon dan D. Linstedt, ed., Data Architecture: a Primer for the Data Scientist, Morgan Kaufmann, Boston. https://doi.org/10.1016/B978-0-12-802044-9.00035-0 ⌃ ⌃²
Li, Q. (13 Maret 2018): Laplacian Smoothing and Graph Convolutional Networks, diperoleh 7 November 2022, melalui situs internet: https://liqimai.github.io/blog/AAAI-18/. ⌃
Makki, M., Showkatbakhsh, M., dan Song, Y. (2019): Wallacei Primer 2.0. ⌃ ⌃² ⌃³
Preim, B., dan Botha, C. (2014): Chapter 6 - Surface Rendering, 229–267 dalam B. Preim dan C. Botha, ed., Visual Computing for Medicine (Second Edition), Morgan Kaufmann, Boston. https://doi.org/10.1016/B978-0-12-415873-3.00006-7 ⌃ ⌃²
Schneider, C., Koltsova, A., dan Schmitt, G. (2011): Components for parametric urban design in Grasshopper from street network to building geometry., 75, 68. ⌃ ⌃²
Xiao, L., Yang, G., Yang, K., dan Mei, G. (2019): Efficient Parallel Algorithms for 3D Laplacian Smoothing on the GPU, Applied Sciences. https://doi.org/10.3390/app9245437 ⌃ ⌃² ⌃³ ⌃⁴ ⌃⁵
Zeng, W., dan Church, R. L. (2009): Finding shortest paths on real road networks: the case for A*, International Journal of Geographical Information Science, 23(4), 531–543. https://doi.org/10.1080/13658810801949850 ⌃